Tries

4th September, 2025

A Trie (pronounced "try") is a tree like data structure that can be particularly useful when working with words and things like autocomplete.

It is a specialized search tree that can be traversed in order to search words from a dictionary or a set efficiently and potentially the rest of the words that can be formed from a search prefix. It is hence also sometimes called a prefix tree as we can use the current search term as the prefix of a word and complete the rest based on words in our trie.

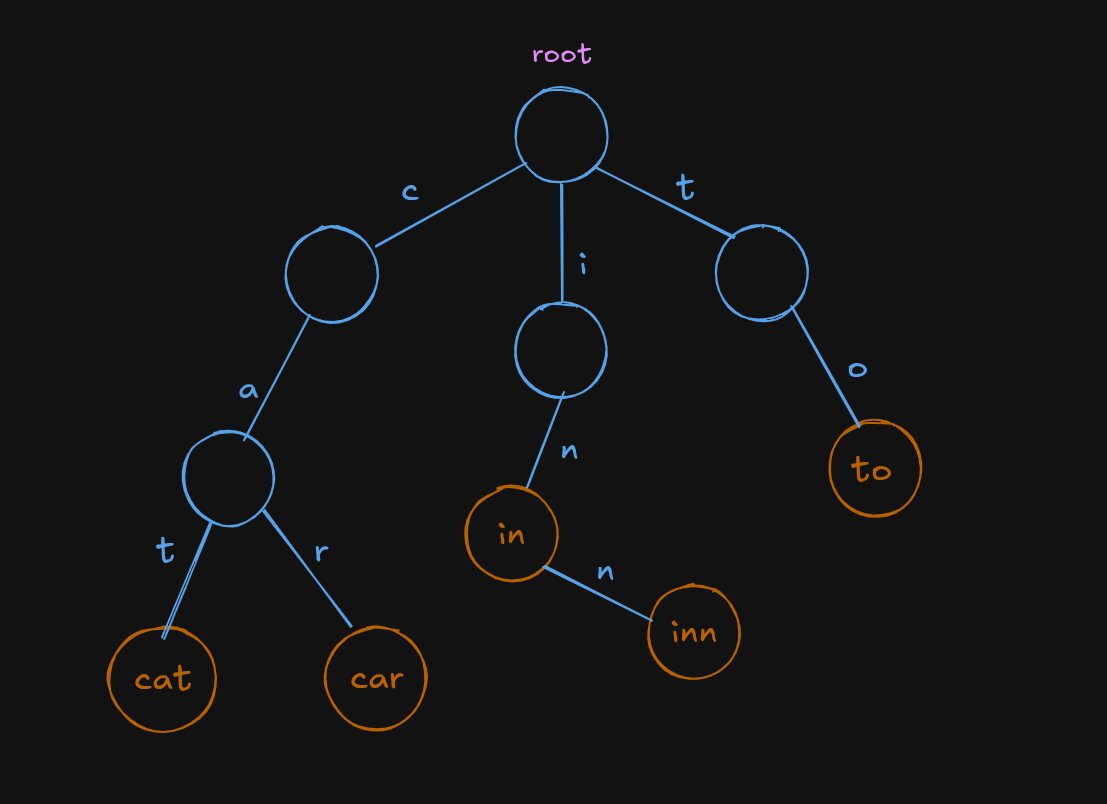
Here's an conceptual picture of a Trie containing the words car, cat, in, inn, to.

Implementation

Let us start with the things we will need to store at each node in our trie. First, we will need to store the valid transitions, i.e. the characters that will be consumed to go from a node to the next. Second, we will need one more property to know whether a node is a terminal node i.e. a word ends at this node or not. This will become handy when storing words that are a prefix to another word, such as in and inn in the above example.

class Trie:
    def __init__(self):
        self.is_terminal = False
        self.children = {} # stores the valid characters for transitions

Let us define some operations on our trie. As per 208. Implement Trie (Prefix Tree) , we are said to implement insert, search, startsWith on our trie. It will be called like so,

Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // return True
trie.search("app");     // return False
trie.startsWith("app"); // return True
trie.insert("app");
trie.search("app");     // return True

Inserting a word can be done by taking the first character, making a node if the node doesn't exist, add the correct children for the next transitions and move to the next node to insert the next character.

    def insert(self, word: str) -> None:
        if len(word) == 0:
            self.is_terminal = True
            return
        f = word[0]
        if f in self.children:
            n = self.children[f]
            n.insert(word[1:])
        else:
            self.children[f] = Trie()
            self.children[f].insert(word[1:])

Searching for a word is easy. We just need to follow character by character and see where the trie takes us. If we reach a node where it is a terminal node, we have stumbled upon a word in our trie and are successful. If we cannot move further and we have not gotten to the end of the word yet, we do not have that word in our trie.

In our recursive solution, we repeatedly take the first character, see that it is a valid transition or not. If so, we move to the next node and attempt to search the rest of the word until we have no more characters. If the first character was not in our children to begin with, we can return False.

	def search(self, word: str) -> bool:
        x = self

        if len(word) == 0:
            if x.is_terminal:
                return True
            else:
                return False

        ch = word[0]

        if ch not in x.children:
            return False

        if len(word) > 0:
            n = self.children[ch]
            return n.search(word[1:])

I think now the startsWith method will become trivial. It is very much similar to the search method, however we do not have to check for a terminal node as we do not need to check for a full word.

    def startsWith(self, prefix: str) -> bool:
        x = self

        if len(prefix) == 0:
            return True

        ch = prefix[0]

        if ch not in x.children:
            return False

        if len(prefix) > 0:
            n = self.children[ch]
            return n.startsWith(prefix[1:])

Slight modifications can be useful

In 211. Design Add and Search Words Data Structure , we can see that a Trie will be useful as most operations are very similar and the usecase fits perfectly. However, we need to accomodate one more thing in our search function, which is the use of a wildcard character .

WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b.."); // return True

We can modify just the portion in search above to make this work.

We can start a BFS or DFS search everytime we hit a . as we do not know by consuming which character we can match the rest of the characters to reach a terminal node.

Here I use a for loop with recursion which acts like a DFS search across all children from a node when the next character in the search term is a .

def search(self, word: str) -> bool:
    if len(word) == 0:
        if self.is_terminal:
            return True
        else:
            return False

    ch = word[0]

    # if . is present, start a search across all children
    if ch == ".":
        is_possible = False
        for _, v in self.children.items():
            result = v.search(word[1:])
            is_possible = result or is_possible
            if is_possible:
                break
        return is_possible
    else:
        if ch not in self.children:
            return False

    if len(word) > 0:
        n = self.children[ch]
        return n.search(word[1:])